 is
a 5-tuple
is
a 5-tuple 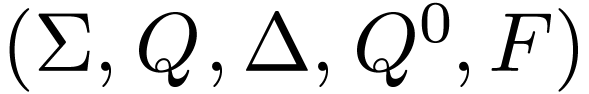 such that
such that
|
In model checking, the system and its corresponding LTL specification are often translated into automata-based models. One of the most popular approach to LTL model checking is an automata-theoretic algorithm called tableau construction. This method take advantage of the fact that both system and its specification can be represented in the same notion, which in here is the Bu¨chi automata model. In this article, we will breifly discuss the properties of Bu¨chi automata, the most widely used automata model in model checking literature. This article assumes you have some basic knowlege on axiomatic set theory and automata theory.
Let us first do a quick recap on your undergraduate theory of computation course. If you have some knowledge on automata theory, you may know that a regular finite automaton, which takes fintie words as input, can be formally defined by a 5-tuple.
Definition  is
a 5-tuple
is
a 5-tuple 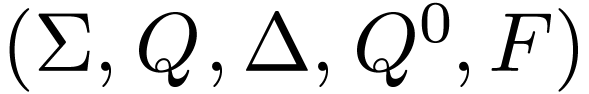 such that
such that
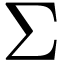 is a finite set of alphabet,
is a finite set of alphabet,
 is a finite set of states,
is a finite set of states,
 is the finte transition relation,
is the finte transition relation,
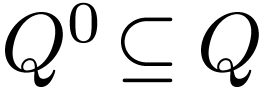 is the set of initial states,
is the set of initial states,
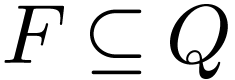 is the set of accepting states.
is the set of accepting states.
Now we can define the notion of a run on a automaton :
Definition 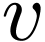 be a word (string,
sequence) in the language
be a word (string,
sequence) in the language 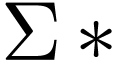 (the
Kleen closure of the alphabet
(the
Kleen closure of the alphabet 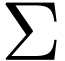 )
of finite length
)
of finite length 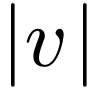 . A run of
. A run of
 over
over 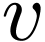 is a mapping
is a mapping 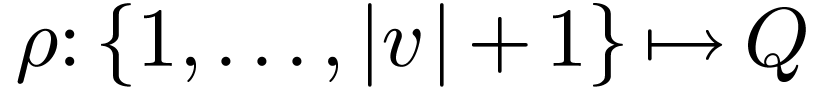 such that the following properties holds:
such that the following properties holds:
The first state 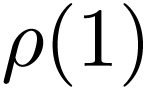 is in the set of initial
states.
is in the set of initial
states.
For 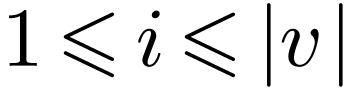 ,
, 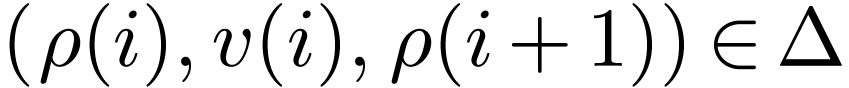 , that is, consecutive states must obey the
transition relation
, that is, consecutive states must obey the
transition relation  .
.
A run 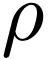 is called accepting if it ends with a
state in
is called accepting if it ends with a
state in 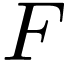 .
.
We define the language 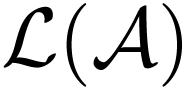 to be the set of all
words accepted by the automaton
to be the set of all
words accepted by the automaton  and is said to
be a Regular Langauge. A regular langauge can be described by a
regular expression, such as
and is said to
be a Regular Langauge. A regular langauge can be described by a
regular expression, such as 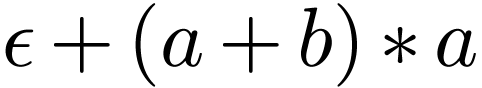 .
This article will not elaborate on the meaning of them, as regular
expression is almost ubiquitous in day-to-day programming.
.
This article will not elaborate on the meaning of them, as regular
expression is almost ubiquitous in day-to-day programming.
Bu¨chi automata can be defined by the same 5-tuple that defines finite automata. In fact, the only difference between Bu¨chi automata and finite automata is that Bu¨chi automata can take words of infinite length as input. Since computers have finite amount of memory and many computer programs only run for finite amount of time, one may argue that finite length input and finite length runs are sufficient to describe the behavior of a system. However, infinite sets (and their cardinalities) can be think of the limit of finite sets when they are bounded but their boundaries are unkown. Furthermore, reactive systems such as traffic light control systems are not expected to terminate. In these scenarios, we must introduce Bu¨chi automata.
Definition  can be infinitely long. That is,
can be infinitely long. That is,  ,
same as the cardinality of the set of all natural numbers.
,
same as the cardinality of the set of all natural numbers.
Unlike finite automata who take words in 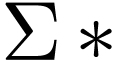 ,
Bu¨chi automata take words in
,
Bu¨chi automata take words in 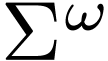 , which is the language of finite and
infinitely long strings whose characters are in
, which is the language of finite and
infinitely long strings whose characters are in 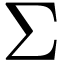 , as input. For a Bu¨chi
automaton
, as input. For a Bu¨chi
automaton  , the langauge
, the langauge 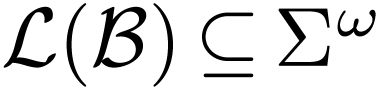 consists of all the words accepted by
consists of all the words accepted by 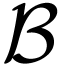 and is called an
and is called an 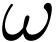 -regular
language. To properly define what it means for a Bu¨chi
automaton to accept a word, we must first prove a preliminary lemma.
-regular
language. To properly define what it means for a Bu¨chi
automaton to accept a word, we must first prove a preliminary lemma.
Lemma 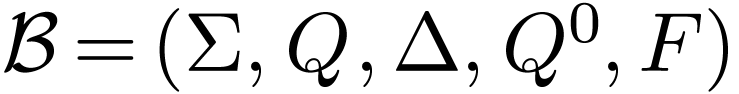 be a Bu¨chi automaton,
be a Bu¨chi automaton, 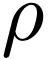 be
an infinite run on
be
an infinite run on 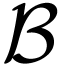 . There
exists a non-empty set of states in
. There
exists a non-empty set of states in  called
called 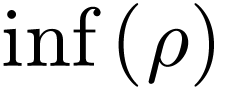 such that it appears infinitly many times in the
right-hand side of the mapping
such that it appears infinitly many times in the
right-hand side of the mapping 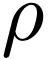 .
.
Proof. By the infinite pigeonhole principle, since 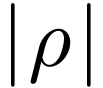 is infinite and
is infinite and  is finite,
there must be at least one state in
is finite,
there must be at least one state in  such that it
appears infinitely many times in the right-hand side of
such that it
appears infinitely many times in the right-hand side of 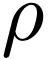 .
.
With the notion of 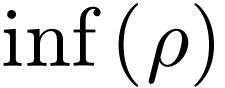 , we can
now define the concept of acception formally:
, we can
now define the concept of acception formally:
Definition 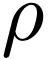 is said to be accepted by
a Bu¨chi automaton
is said to be accepted by
a Bu¨chi automaton 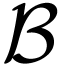
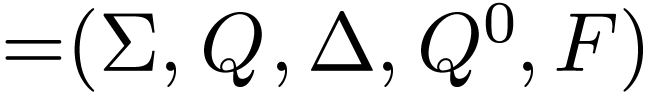 if and only if
if and only if  .
.
Note that this definition is very similar to how we define fairness in LTL, in fact the fairness condition in LTL is called generalized Bu¨chi acceptance condition.
An important difference between regular finite automata and Bu¨chi automata is that non-deterministic Bu¨chi automata are strictly more expressive than deterministic ones.
Remark  is actually a
partial function
is actually a
partial function 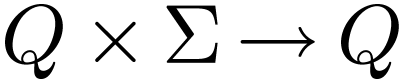 , that is,
given a state and a character in alphabet, there is at most one next
state. Non-deterministic Bu¨chi automata do not
have this limitation.
, that is,
given a state and a character in alphabet, there is at most one next
state. Non-deterministic Bu¨chi automata do not
have this limitation.
Lemma  be a deterministic Bu¨chi
automaton. Then
be a deterministic Bu¨chi
automaton. Then 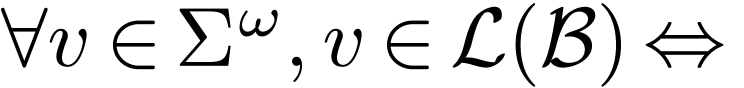 there is an
infinite set of prefixes of
there is an
infinite set of prefixes of 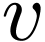 on which
on which 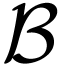 reaches an accepting state.
reaches an accepting state.
Proof. For deterministic Bu¨chi
automata, one input word can have exactly one run starting from its
initial state. Thus this proposition can be proved directly from the
definition of acception. 
Theorem
Proof. Consider the language 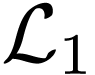 whose
whose 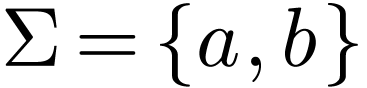 and consists of finite number of
and consists of finite number of 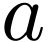 's but infinite number of
's but infinite number of 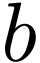 's . We will prove that no
deterministic Bu¨chi automaton can accept this
language.
's . We will prove that no
deterministic Bu¨chi automaton can accept this
language.
Suppose there exists such automaton 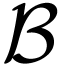 such that
such that
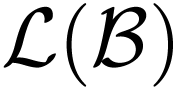 equals
equals 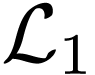 .
By the definition of
.
By the definition of 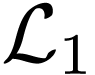 , for
any finite word
, for
any finite word 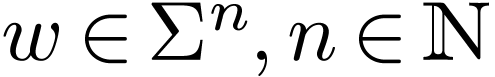 , we have
, we have
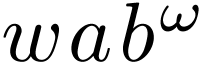 in
in 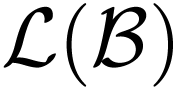 .
Now we can construct an infinite sequence of words
.
Now we can construct an infinite sequence of words 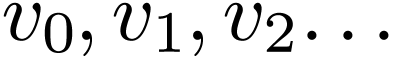 such that
such that 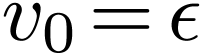 ,
, 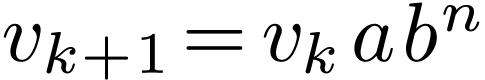 ,
, 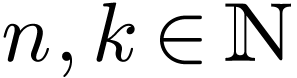 where
where 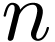 is the smallest natural number such that
is the smallest natural number such that 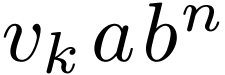 is in
is in 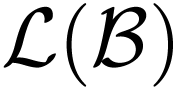 . Following this
definition, we can construct a function
. Following this
definition, we can construct a function 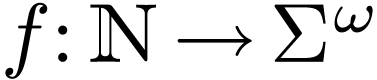 that
maps a natural number to a word
that
maps a natural number to a word 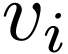 .
Let infinite word
.
Let infinite word 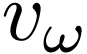 be any infinite word accepted
by
be any infinite word accepted
by 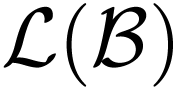 such that all words in
such that all words in 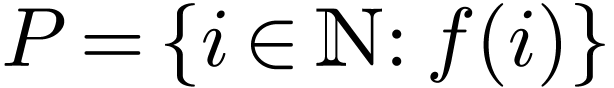 are its prefixes. By lemma 7, this word
are its prefixes. By lemma 7, this word 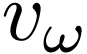 is accepted by
is accepted by 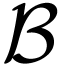 . However, for
any finite number
. However, for
any finite number 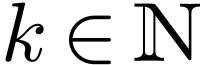 , there is
always a prefix of
, there is
always a prefix of 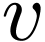 having
having 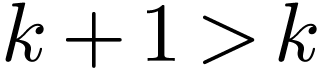 many of
many of 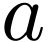 's. Therefore
's. Therefore 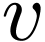 contains infinitely many
contains infinitely many 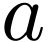 's, contradicting the definition of
's, contradicting the definition of 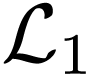 .
.
However, there exists a non-deterministic Bu¨chi
automaton that accepts this language, see figure 1.
 |